
La vaca esférica
Los tres iconos de la comedia en Física según la APS
La vaca esférica es la mascota preferida de los físicos. Es tan famosa que cuando la Sociedad Americana de Física decidió hacer camisetas para sus socios en 2013 a la vaca la pusieron en el centro, entre el gato de Schrödinger y el electrón en un bar. A veces se utilizan otros animales de ejemplo como los pollos, pero los físicos de verdad no aceptamos imitaciones: sabemos que tienen que ser vacas o no funciona igual =).
Sentimos cariño por la vaca esférica porque nos ha acompañado toda la carrera, pero sobre todo porque representa lo más alucinante de la Física: que funcione. Y es que nuestros modelos físicos son en muchos casos burdas aproximaciones de la realidad, pero resulta que con ellos podemos reflejar de una forma extraordinaria lo que sucede en la naturaleza, algo que expresó como nadie Bertrand Russell:
La conclusión final es que sabemos muy poco y sin embargo es asombroso que sepamos tanto, y más sorprendente aún que tan poco conocimiento nos dé tanto poder.
La vaca esférica¹ representa esos modelos teóricos de servilleta, demasiado simplificados, ingenuos, torpes. Modelos de juguete en muchos casos…, pero con una gran virtud: permiten hacer cálculos y predicciones, permiten comprobar hipótesis, permiten avanzar en nuestro conocimiento.
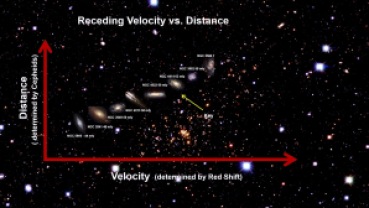
La ley de Hubble
Se me ocurren varios ejemplos de vacas esféricas, pero quizá una de las que más me asombró en su día fue la ley de Hubble. Edwin Hubble (1889-1953) propuso en 1929 que la velocidad a la que se alejan las galaxias de nosotros es proporcional a la distancia que nos separa de ellas. O lo que es igual, las galaxias más distantes se alejan de nosotros a más velocidad que aquellas que están cerca (la constante de proporcionalidad vale unos 71 km/s/Mpc). El enunciado puede parecer muy simple pero no os engañéis: fue la primera prueba experimental del Big Bang y supuso un enorme paso en nuestra comprensión del Universo. El caso es que, cuando se echa un vistado a los datos de los que Hubble disponía lo que aparece es una pequeña nube de puntos con una tendencia ascendente. El rango de distancias y velocidades que él pudo investigar era relativamente bajo (unos 2 Mpc y 1000 km/s), y cuando se compara con los datos actuales se puede decir que lo que tenía era más bien un modelo optimista (aunque era el único razonable). Pero es que contar galaxias no es algo sencillo.

Comparación del modelo de Hubble en 1929 con los datos de 1996.
Hoy me ha tocado contar objetos físicos, y me he sentido un poco como Hubble. Me he encontrado con pocos puntos en mi gráfica… Bueno, en realidad me he quedado con ¡un solo punto! Y es que hay problemas físicos cuya complejidad escala extremadamente rápido con el número de partículas, y si no me creéis intentad doblar una hoja de papel por la mitad más de 7 veces…
Pero a mí no me ha tocado contar galaxias, sino iones. Veréis, yo necesitaba calcular la distribución de iones (y de átomos desplazados) durante un proceso de implantación. La implantación iónica es un proceso que se usa para modificar las propiedades de los materiales, especialmente de los semiconductores. Se lanza un ion muy rápido contra el material y éste entra como una bala hasta que se queda dentro (implantado). La profundidad a la que se implanta depende de la energía de la bala, claro. Las energías necesarias para modificar la superficie de un material no son muy altas (keV), pero aún así hace falta un acelerador de partículas.

Esquema de un implantador de iones (Fuente: desconocida)
El caso es que si se implantan muchos iones se pueden cambiar las propiedades del material. Por ejemplo, transformar algo aislante en conductor, algo transparente en opaco, o algo no magnético en magnético. Pero claro, para eso hacen falta muchos iones. ¿Cuántos? Pues yo trabajo con silicio pata negra, que tiene por término medio 5·1022 átomos por centímetro cúbico. Para conseguir que el silicio tenga un buen grado de conductividad hacen falta cerca de 1015 iones por cm³. Eso es un número ridículamente pequeño para los átomos de silicio del cristal (sólo hay 2 iones implantados por cada 100 millones de átomos de Si), pero es un número tremendamente alto para implantar. Si mandáramos uno cada segundo necesitaríamos 317 millones de años para implantarlos todos.
Pero mi problema no eran los iones: los iones podemos implantarlos sin problema y no necesitamos esperar tanto tiempo. El problema aquí es que cada ion que entra en el cristal de silicio se cepilla todo lo que se encuentra por el camino (al fin y al cabo es una bala). Esto, en términos científicos, se llama daño nuclear causado por cascadas de colisiones. Cuando el ion se encuentra de frente con un átomo, lo desplaza, y ése a su vez desplaza a otro, y ése a otro, como en el billar. Y eso era justo lo que yo tenía que contar: yo tenía que seguir cada uno de los átomos de silicio desplazados y calcular el promedio de sus desplazamientos.

Las cascadas de colisiones de un ion son como las del billar. (Fuente de la foto: Wikipedia)
Evidentemente esto no se hace a mano. Tenemos programas Monte Carlo que simulan las trayectorias de los iones. Los programas Monte Carlo utilizan métodos aleatorios para simular procesos complejos y muy costosos de calcular, pero aún así tienen sus límites: no podemos simular 1015 iones. Como mucho podemos alcanzar el millón de partículas en un ordenador normal, aunque yo decidí empezar de manera modesta para ahorrar tiempo. Me sentía optimista, como Hubble, así que fijé el número de iones en N=1000. Unos minutos viendo la lluvia de iones en mi ordenador y voilà. Mil iones lanzados. Fichero de salida: 100 megas de puro texto. Debería haber sospechado algo en ese momento pero estaba lleno de confianza: abrámoslo… Uy, peta el ordenador.

Histograma de iones de Fe implantados en Si simulados por Monte Carlo. La profundida media es de 38.7 nm.
Mi problema físico se acaba de convertir en un problema informático de memoria RAM, así que bajo un orden de magnitud: N=100. ¡Ajá! Ahora ya sólo tarda 3 segundos en abrir el archivo. Pero tiene más de ¡140.000 líneas! y el formato sigue siendo intratable. Las cascadas de colisiones están agrupadas y necesitaría días para separar todos los átomos que busco para mi estadística. Voy al final del archivo y descubro el problema: cada ion genera demasiados desplazamientos atómicos. Bajar a N=10 mejoraría la situación, pero a mí se me acaba el tiempo y hay que tomar una decisión rápida.

Me vienen a la cabeza las clases de Métodos de tercero, donde me dijeron que, gracias al teorema central del límite, la vida se vuelve gaussiana con muy pocos datos y que en muchos casos 10=∞ (esto es literal). Así que, ¿por qué no? Invoquemos a la vaca esférica. Simplificación máxima del problema: N=1. Como lo oís. Voy a simular un solo ion. La simulación es instantánea, por supuesto, y abrir el archivo también. A pesar de eso me toca filtrar 1400 líneas. Separo las cascadas por orden y las coloco en función de su profundidad.

Implantación de 1 ion de Fe (línea roja) en Si con sus 65 cascadas de colisiones (1024 átomos desplazados). Mi modelo de vaca esférica.
Ahora sí. Mi ion (en rojo) había acabado a una profundidad de 61.3 nm, bastante por encima de la media, pero lateralmente no se había desviado mucho (sólo 11.7 nm). El azar ha querido que haya 65 cascadas de colisiones, y que la más grande haya provocado 389 desplazamientos. Sólo tengo un ion, pero ese ion ha movido 1024 átomos de su sitio él solito. Me dispongo a contar los heridos y a hacer mi estadística. 1024 ya es un número manejable. La vaca esférica ha triunfado una vez más, y yo hoy podré irme a casa a dormir. =D
@DayInLab
¹ En realidad, el origen de la vaca esférica se encuentra en el libro de John Harte titulado Consider a Spherical Cow: A Course in Environmental Problem Solving, donde se menciona esta historia:
La producción de leche de una granja era tan baja que el granjero pidió a la universidad local ayuda académica. La universidad reunió un equipo multidisciplinar de profesores, encabezado por un físico teórico, y estuvieron dos semanas haciendo investigación de campo intensiva. Los científicos volvieron a la universidad, con sus portátiles repletos de datos, y el encargo de escribir el informe se dejó para el líder del equipo. Poco después, el físico volvió a la granja y le dijo al granjero: «Tengo la solución pero sólo funciona para vacas esféricas en el vacío».

I knew this one with a chicken actually… But didn’t know the origin, so thanks again for educating us!
BTW, do you know that of the photon checking in at the hotel?
[…] defensa de los problemas de Fermi, de las preguntas inútiles, de la imaginación, los juegos y las vacas esféricas. Y es que, cada vez siento que hacen más falta en la vida de los físicos o, por lo menos, de los […]