Dirac, ¿y eso para qué sirve?

Dirac, ¿y eso para qué sirve?

/ 15 mayo, 2015 / 30 Comments / Blog del Lab

En mi primera entrada del blog prometí que algún día os hablaría de mi momento preferido de la ciencia y hoy ha llegado el día porque Nuria lo ha contado tan bien en la final de Famelab que a partir de ahora la gente sólo querrá ver su video… =)

Es una historia que he contado muchas veces porque como profesor siempre me he tenido que enfrentar a la desagradable pregunta: «¿y eso para qué sirve?» Desgraciadamente vivimos en una sociedad en la que se da valor sólo a lo inmediato y a lo material, así que no se aprecia para nada el conocimiento, que no es ni una cosa ni la otra. Existe además la ridícula idea de que hay que justificar el conocimiento con la utilidad, cuando el conocimiento debería ser un fin en sí mismo. Esta entrada va para todos aquellos que alguna vez preguntaron «¿y eso para qué sirve?». Si leéis la entrada hasta el final os garantizo que jamás volveréis a preguntarlo.

Dirac

P.A.M. Dirac (1902-1984)

El protagonista de mi historia es Paul Adrien Maurice Dirac, y tendréis que viajar a los primeros años del siglo XX para entenderla. En esa época dos revoluciones científicas sin precedentes se producían casi simultáneamente en la Física. Por un lado, Albert Einstein había publicado su famosa teoría especial de la relatividad, donde se rompía con los conceptos de espacio y tiempo absolutos, un principio básico de la Física de Newton al que tendríamos que renunciar desde entonces. Por otro lado se descubrían las increíbles propiedades de la materia a escala atómica con el nacimiento de la mecánica cuántica. Sus cuatro características más sorprendentes eran la ubicuidad (una cosa puede estar en varios sitios -estados- al mismo tiempo), el no determinismo (al medir algo se pueden obtener resultados diferentes aleatoriamente), la no-localidad (lo que pasa en un sitio puede afectar a sitios lejanos instantáneamente) y la incertidumbre (no se pueden conocer con precisión dos propiedades relacionadas entre sí).

Este cambio en las reglas del juego de la Física supuso una renovación conceptual muy difícil y no fue algo inmediato ni mucho menos. En algunos aspectos las dos nuevas teorías no se llevaban bien (la relatividad al fin y al cabo no era tan radical como la cuántica) y costó mucho reconciliarlas… hasta qué llegó Dirac.

Desintegracion

La desintegración de la persistencia de la memoria (1931). Dalí se inspira en las dos teorías físicas más revolucionarias del siglo XX: la relatividad y la mecánica cuántica.

En 1928 Dirac se propuso encontrar la ecuación del electrón libre relativista, porque la ecuación de Schrödinger no cumplía con los requisitos de la teoría de Einstein¹, es decir, no trataba por igual espacio y tiempo, y no incorporaba la energía en reposo (el famoso E=mc²). Además de eso no explicaba el espín, una propiedad fundamental de las partículas sin equivalencia clásica, pero que separa la naturaleza en dos familias totalmente distintas: bosones (como el fotón, de espín entero) y fermiones (como el electrón, de espín semientero). Para los que no sois físicos el espín os resultará una tontería pero debéis saber que es tan importante que las fuerzas de la naturaleza se transmiten sólo por bosones, mientras que las partículas más elementales están formadas sólo por fermiones.

Espín

El espín es una propiedad interna de las partículas que refleja una simetría fundamental de la naturaleza explicada por la ecuación de Dirac

Para devolver a la ecuación de Schrödinger su carácter relativista Dirac tuvo que hacer varias transformaciones e incluir cuatro nuevas constantes (las matrices α), totalmente independientes de las variables espacio-tiempo y del momento de la partícula. Eso quería decir que representaban un grado interno de libertad, una característica intrínseca de la partícula como la masa, pero una característica nueva.

0417b5446909116f3142990205815417

Ecuación de Dirac

Dirac estudió sus propiedades y encontró que tres de esas constantes (α1, α2, α3) ¡eran precisamente las matrices de Pauli! que describen las tres componentes de espín del electrón. Esto era algo grande, verdaderamente asombroso, porque explicaba por primera vez el origen del espín como una necesidad de la naturaleza para mantener la simetría espacio-tiempo de la relatividad en mecánica cuántica.

Dirac's_commemorative_marker

Lápida de Dirac en la abadía de Westminster

Pero quedaba todavía una constante más (α0), y una sorpresa mayor. Esta constante estaba relacionada con la energía en reposo de la partícula, y sorprendentemente podía tomar valores positivos (lo esperado para el electrón, +mc²) pero también ¡¡¡valores negativos!!! (-mc²). Esto era totalmente insólito. Dirac andaba buscando una solución positiva (la del electrón), pero se topó con dos, y una de ellas parecía tener energías negativas. Era el equivalente a hacer la raíz cuadrada de 4; tienes la solución normal (+2) pero también otra inesperada (-2).

Dirac entendió pronto que su ecuación predecía una nueva partícula, que era una especie de antielectrón, con las mismas propiedades pero con carga positiva y una energía negativa. Su primer intento fue identificar esa partícula con el protón pero había varios argumentos en contra (la partícula tenía que ser exactamente de la misma masa que el electrón, y el protón es unas 2000 veces más pesado). Así que Dirac acababa de dar con una partícula que experimentalmente jamás se había detectado.

Dirac seguía unos principios matemáticos muy claros y estaba seguro de que su ecuación era correcta:

Este resultado es demasiado bello para ser falso. La belleza de una ecuación es más importante que ajustarse al experimento.

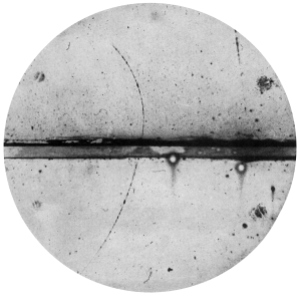
PositronDiscovery

Traza de un positrón encontrada por Anderson: la primera evidencia experimental de antimateria

Tenía razón. Tan sólo cuatro años más tarde, Carl David Anderson (1905-1991) estaba fotografiando las trazas de partículas producidas por rayos cósmicos en una cámara de ionización cuando encontró una partícula con la masa del electrón, pero con carga positiva. ¡Exactamente lo que Dirac había predicho! A esa partícula se le dió el nombre de positrón y fue la primera evidencia experimental de que la antimateria existía.

Aniquilacion

La aniquilación de un electrón y un positrón emite simultáneamente dos fotones de 511 keV en sentidos opuestos

La antimateria es exactamente igual que la materia ordinaria, sólo que con algunas propiedades cambiadas como la carga o el espín. Sin embargo, cuando una partícula se encuentra con su antipartícula se produce un fenómeno físico de aniquilación, en el cual ambas partículas desaparecen liberando una gran cantidad de energía. Por ejemplo, cuando un electrón se encuentra con un positrón ambas partículas se desintegran produciendo dos fotones de 511 keV de energía.

Por alguna razón que no esta todavía clara el mundo en el que vivimos está formado casi exclusivamente por materia ordinaria. La antimateria sólo se produce en ciertas desintegraciones radiactivas o artificialmente en aceleradores de partículas. Se calcula que, desde su descubrimiento, sólo se ha producido 1 nanogramo de antimateria. No obstante, existen instalaciones como el ALPHA del CERN donde se producen (y se intentan atrapar) antiátomos.

PET_anime

Tomografía por emisión de positrones de un paciente

Pero diréis… Todo esto es muy bonito, pero sigues sin decirme para qué sirve. Y es verdad. Hasta ahora sólo os he hablado de un descubrimiento revolucionario: el de encontrar antimateria en el Universo. Pero esto no era más que conocimiento, sin ninguna utilidad práctica. Y es que muy frecuentemente la ciencia va por delante de la tecnología, así que las aplicaciones llegan siempre después: cuando se ha entendido de verdad lo que pasa. ¿Queréis saber para qué sirve la antimateria? Mirad a la derecha…

Lo que estáis viendo es una reconstrucción 3D de un paciente hecha con tomografía por emisión de positrones (PET). Voy a repetirlo: PO-SI-TRO-NES. Y voy a repetirlo todavía otra vez más: PO-SI-TRO-NES. Esos positrones que ni siquiera sabíamos que existían hasta que llegó Dirac, esos positrones que no eran más que pura teoría hasta que los descubrió Anderson, esos mismos positrones que prácticamente no existen en nuestro mundo repleto de materia normal… Resulta que hoy en día sirven para la detección de tumores.

Ya, ahora querréis saber cómo, ¿verdad? Bueno, si habéis llegado hasta aquí os lo merecéis. La idea física es la siguiente: sabemos que cuando un positrón se encuentra con un electrón se aniquila emitiendo dos fotones exactamente idénticos (de 511 keV), pero en sentidos opuestos. Pues bien, si detectamos esos dos fotones en coincidencia (es decir, que sabemos que se han producido a la vez) podemos reconstruir el origen de la aniquilación y determinar con bastante precisión el lugar en el que se ha producido. Esa aniquilación no ocurre prácticamente nunca en nuestros cuerpos porque estamos formados sólo por vulgares electrones, pero ¿y si nos inyectaran positrones?

tep

Funcionamiento básico de la tomografía por emisión de positrones (Imagen de Wikipedia)

Inyectarnos positrones no es tan sencillo porque no se venden en pastillas, pero se puede hacer. En realidad lo que se hace no es inyectar directamente positrones, sino inyectar un radioisótopo que se desintegra emitiendo positrones. El isótopo más fácil de producir con esas características es el Flúor-18 (que se obtiene por transmutación del Oxígeno-18 usando ciclotrones²). El Flúor-18 tiene además una gran habilidad: puede unirse a la glucosa formando un compuesto denominado fluorodesoxiglucosa (18FDG). Y la glucosa es una molécula que nuestro organismo consume de manera natural por lo que puede usarse como marcador o trazador en el paciente. ¿Qué sucede entonces cuando se introduce ese marcador radiactivo en tu cuerpo?

220px-Fluorodeoxyglucose

Molécula de fluorodesoxiglucosa usada en el PET

Sucede que la glucosa es el combustible típico de nuestros órganos, especialmente de nuestro cerebro, porque proporciona mucha energía. Ahora bien, cuando se produce un crecimiento o una reproducción exageradamente alta de células (como en un tumor), hay un consumo anormal de glucosa, lo que hace que nuestro marcador se fije, principalmente, en esas zonas. Como nuestro marcador está lleno de Flúor-18 los positrones se emitirán mayoritariamente en esas regiones de nuestro cuerpo. Tan pronto como se emitan serán aniquilados por los electrones más cercanos, y sus dos fotones en coincidencia nos dirán dónde ha sido eso.

pet_scan_2

Máquina de PET comercial

Evidentemente, para que todo esto sea posible hoy hizo falta el desarrollo de muchas partes de la ciencia: detectores de rayos gamma, electrónica de adquisición rápida, técnicas de reconstrucción de imágenes, producción de radioisótopos con aceleradores a nivel industrial, medicina nuclear… Pero nada, nada de esto habría servido si Dirac no se hubiese sentado un día a unificar la relatividad y la mecánica cuántica en una ecuación y hubiese descubierto la antimateria.

Así que la próxima vez que vayáis a preguntar despectivamente «¿y eso para que sirve?», pensádlo dos veces. Lo que hacemos los científicos puede que no sirva para nada hoy, pero quizá algún día te salve la vida³. Y si no me creéis a mí, por lo menos creed a Nuria, que ella sí que sabe…

 

¹ En realidad Schrödinger obtuvo primero la ecuación relativista, hoy conocida como ecuación Klein-Gordon, pero la descartó por no explicar los resultados experimentales conocidos.

² Los ciclotrones son aceleradores de partículas circulares. Como curiosidad el primer acelerador de partículas del mundo, construído por Ernest Lawrence en 1932 era un ciclotrón.

³ Por si después de esta entrada aún hay alguien que no esté convencido recomiendo la excelente charla «El huevo y la niña» de José Manuel López Nicolás.

Etiquetas: , , , , , , , , , ,