
La sensación de poder (tributo a Asimov)
Hay un relato corto de Asimov que me gusta mucho titulado La sensación de poder, y que podéis leer aquí, aunque lo mejor es que os compréis los Cuentos Completos, que no tienen desperdicio. El relato habla de la maravillosa sensación que es saber y aprender, usando para ello una ingeniosa historia que cada día es más actual, y que él publicó antes de que se inventaran las calculadoras de bolsillo. Hoy he recordado ese cuento porque voy a hablaros precisamente de un momento parecido que me ocurrió en el laboratorio.
Mi historia empieza con un experimento de canalización iónica, que como ya habréis oído por ahí es mi fenómeno físico favorito. La canalización consiste en que, cuando se bombardea un cristal con iones, estos pueden penetrar por los huecos alineados de la red cristalina y desvelar cualquier impureza que se encuentre allí chocando directamente con ella. También pueden decirnos la simetría del cristal observando la cantidad de iones que vuelven dispersados en función de la orientación en la que esté.
Pues bien, en este experimento me habían dado para medir un cristal de óxido de zinc (ZnO), pero uno crecido en una orientación difícil. Y es que el óxido de zinc tiene una estructura hexagonal (wurzita), lo que hace que le guste crecer más hacia arriba que hacia los lados. Crecerlo hacia arriba (lo que llamamos en un plano c) es fácil, como demuestran los nanohilos del tipo Burj Khalifa, mientras que crecerlo en las otras direcciones (lo que llamamos plano a y plano m) es complicado y normalmente el cristal se llena de defectos y se estropea.
Pero sí, esta vez me tocaba medir un cristal de plano m. Como nunca había medido esa dirección tuve que usar un programa de cristalografía para saber la simetría que debía esperar, porque un mismo cristal tiene simetrías diferentes dependiendo de por dónde lo mires. No obstante, lo bueno que tienen los cristales es que son periódicos: sólo hace falta conocer su celda unidad (la unidad de repetición más pequeña) para reproducir el cristal entero.
Para averiguar la simetría de un cristal en una determinada dirección usamos una herramienta matemática conocida como proyección estereográfica. La proyección estereográfica se encarga de transformar una cosa que es tridimensional (el cristal) en un mapa bidimensional que contiene la información básica del cristal. La forma de hacerlo es meter la celda unidad del cristal en una esfera y marcar sus direcciones principales sobre esa esfera. Luego se proyectan esos puntos uniéndolos con los polos (primero con uno y luego con otro para no dejarnos puntos), y el corte con el plano ecuatorial nos da un mapa 2D que llamamos estereograma. Un mapa raro, eso sí.
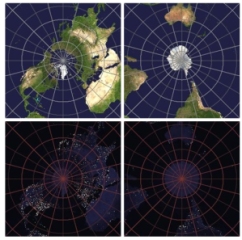
La Tierra proyectada estereográficamente sobre el polo N y el polo S, de día y de noche (Fuente: NASA)
La ventaja de la proyección esterográfica es que, aunque no conserva las distancias reales, sí conserva los ángulos (esta entrada de gaussianos demuestra sus propiedades fundamentales para los más curiosos). Así, mirar el estereograma es como mirar los ángulos principales de rotación del cristal, y resulta muy fácil medir la separación entre distintos planos o ejes. Esto nos permite navegar por el cristal sin perdernos, al igual que los grandes descubridores navegaban por el globo usando sólo el astrolabio.
Para los que estéis pensado que todo esto es muy complicado os voy a confesar que yo saqué un 3 en concepción espacial en el test del colegio… ¡un 3 sobre 100! Así que si yo he podido entenderlo es que es posible. Como ejemplo de un estereograma os dejo aquí el mapa de un cristal con estructura diamante a lo largo de uno de sus ejes (el <100> para ser exactos).

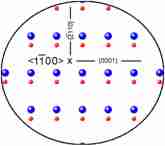
Proyección estereográfica de una red cristalina de tipo diamante. Los círculos más grandes indican las direcciones prinicipales.
Precioso, ¿verdad? Como véis hay direcciones del cristal que son mucho más intensas (los círculos grandes), porque sus canales son muy anchos y canalizar los iones por ellos es mucho más fácil. Las líneas que unen los puntos son planos cristalográficos. Así, por ejemplo, si os fijáis en el círculo central <100> veréis que hay 4 rectas principales que lo cortan, y estas rectas aparecen cada 45º. Eso nos indica, que el cristal tiene simetría cúbica en esta dirección. Se puede hacer lo mismo con cualquier otro eje. Por ejemplo, si buscáis el <110> veréis que también tiene 4 planos que lo cortan, aunque eso no pasa siempre. ¿Podéis encontrar alguno que sólo tenga 3 planos cortándolo? Habréis dado con el <111>, que tiene simetría hexagonal en vez de cúbica.
Ahora ya sabéis cómo averiguar la simetría del cristal sin hacer el experimento. Basta conocer la celda unidad del cristal y algunas matemáticas. Pero yo tenía además que hacer el experimento, y nada te garantiza que el cristal que te venden como perfecto lo sea.
Como anécdota, mi amiga Verónica crecía cristales de CdTe durante su tesis y juraba que eran los mejores del mundo. Nos llevó dos días de experimento conseguir alinearlos porque tenían el eje de simetría desviado más de 5º. Pensad cuánto son 5º y os daréis cuenta de lo difícil que es hacer este tipo de experimentos. Afortunadamente contamos con un goniómetro de precisión, que es un sistema de posicionamiento de muestras que nos permite girar el cristal en los 3 ejes con ¡un error de 0.01º!
En fin, hice el experimento de canalización para ver la simetría del cristal. Lo que ocurre si el cristal es bueno, es que al rotarlo 360º cerca de su eje de simetría debes encontrar todos los planos que lo cortan. Cada vez que se pasa por un plano tiene que aparecer un mínimo de cuentas porque los iones penetrarán por el cristal sin colisionar y al detector de partículas no le llegarán iones dispersados. De esta forma a medida que rotamos el cristal aparecen valles de intensidad, que nos indican que los iones canalizan bien, y que nos dicen dónde están los planos.
Después de hacer el experimento me dí cuenta de que el cristal era pata negra, porque no sólo era capaz de ver sus planos principales, sino también los secundarios. Prácticamente nadie en el mundo crecía este tipo de material así que yo estaba muy ilusionado, pero para poder demostrar que el cristal era tan bueno no me bastaban los estereogramas: tenía que hacer una simulación Monte Carlo y probar que la intensidad de los valles era la correcta.
Eso signficaba que tenía que incluir una nueva celda del cristal en el código, porque jamás habíamos usado este eje. Para ahorraros tiempo os diré que el proceso es realmente complicado y me llevó meses de trabajo. Hay que crear el cristal de cero para que los iones vean exactamente lo mismo que en la realidad y que el potencial eléctrico que sienten sea idéntico. Hacen falta muchas pruebas, y lo peor de todo es que cuando acabas no sabes si lo has hecho bien.
Pero yo tenía mi cristal medido ¡y por fin podía comparar mis simulaciones directamente con el experimento! Así que después de muchos meses de trabajo hice mi simulación, 5000 iones por punto, con cuidado para que fuera comparable a los datos que había tomado, y la pinté corriendo. Tenía buena pinta, pero tenía que superponerla a los datos para saber si estaba bien. Lo hice y… ¡Mierda!: no casaba, porque el cero del experimento no cuadraba con el de la simulación. Sin embargo eso era algo fácil de solucionar. Ahora sí. ¡Ya estaba la gráfica! Simulación contra Experimento, la forma en la que la ciencia avanza y prueba sus ideas. Era la hora de la verdad.
Y sobre la pantalla de mi ordenador de repente vi esto:
¿No es para llorar? Ahí estaba la prueba de que los átomos del cristal estaban perfectamente colocados. Las intensidades simuladas y experimentales se ajustaban asombrosamente bien. El acuerdo era fabuloso. Después de tanto tiempo luchando con los cálculos, de todos los ensayos y errores, después de las medidas y las dudas… os aseguro que aquello fue una maravillosa sensación de poder.







Un relato casi tan top como la canalización iónica.
Hoy he experimentado algo parecido con mi (súper) gráfica de resistividades. Sí que daban ganas de llorar :’)
[…] en particular, el maravilloso acuerdo entre la teoría y el experimento (que me recuerda a La sensación de poder). Sin embargo, las ondas gravitatorias pueden ser tan poco intensas y frecuentes que no volvamos a […]
[…] en particular, el excelente acuerdo entre la teoría y el experimento (que me recuerda a La sensación de poder). Sin embargo, las ondas gravitatorias pueden ser tan poco intensas y frecuentes que no volvamos a […]
[…] los parámetros atmosféricos con la resistencia de nuestra muestra y entonces tuvimos otra sensación de poder, lo vimos claro: habíamos creado un ¡maravilloso sensor de humedad! La humedad relativa también […]
[…] funcionó muy bien la divulgación escrita; libros como Cien preguntas básicas sobre la ciencia de Asimov. Dicho sea de paso, ese libro era una recopilación de entradas de 500 palabras que Asimov […]
[…] que tuvo Asimov cuando aprendió a leer por sí mismo con 4 años, pero tuvo que ser una gran sensación de poder. Tampoco puedo imaginar las magistrales clases que se perdieron los alumnos de la Universidad de […]
[…] sombra de los átomos y la sensación de poder […]
[…] libres genera dudas sobre hasta qué punto deberíamos confiar en los acuerdos numéricos entre teoría y experimento como evidencia para la veracidad de la teoría. Estamos acostumbrados a estas […]